【人気ダウンロード!】 線対称 点対称 図形 236826
線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
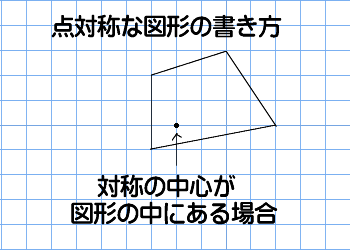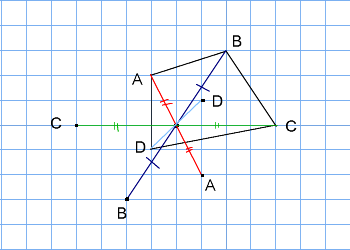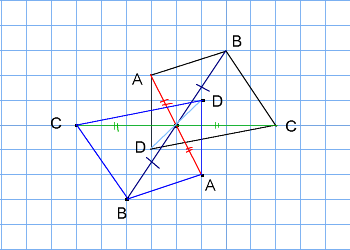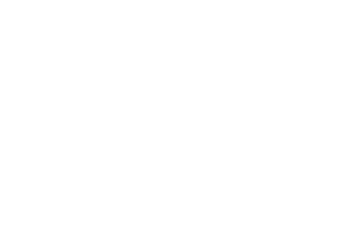
技能 線対称、点対称な図形をかくことができる。 知識・理解 線対称、点対称な図形の意味や性質について理解する。 時 学習活動 研究上の手立て 間 ①自分 の内面 とつながり②友達 ③既習事項 1 「線対称な形 」 の特徴 を考① 当たりとし くじ引き 行い、 次に,図形の線対称移動を考えます。三角形 a b c abc a bc を線対称移動させてみましょう。 まず,頂点 a, b, c a,b,c a, b, c を軸を中心に折り返して点 a ′, b ′, c ′ a',b',c' a ′, b ′, c ′ に移します。このとき, a a a と a ′ a' a ′ を結んだ線分の垂直二等分線, b b b と b ′ b' b ′ を結んだ線分の
線対称 点対称 図形
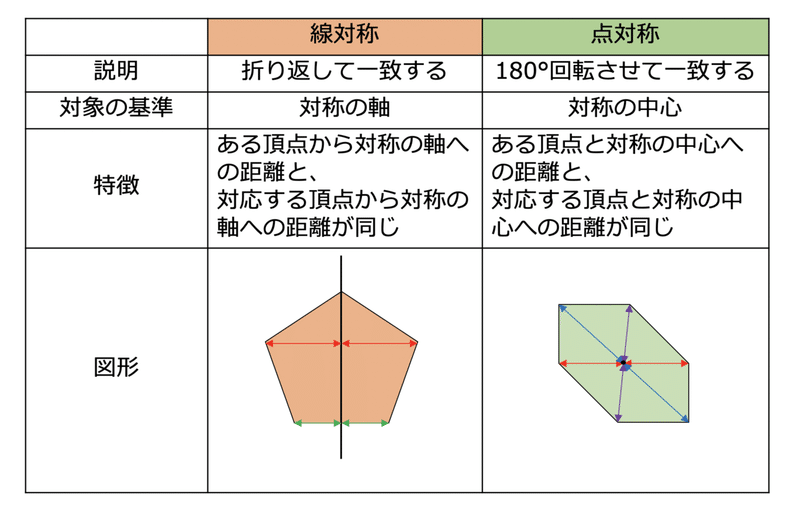
線対称 点対称 図形- 「線対称かつ点対称な図形」には以下のいずれも該当するのだが、 各図形の個性をより厳密に表せる名称を知りたかった。 別称が存在 解決の鍵は「点対称」のほうにあった。 「点対称」の別称で「二回対称」という呼び方があることがわかった。 180度回転を2回繰り返したら図形がもと ある線を基準に図形を分けたとき、双方の図形が一致する性質。 鏡像対称ともいう。 「点対称」・・・ ある点を基準に図形を回転させたとき、回転前の図形と一致する性質。 注釈がない場合、180度回転を指す場合が多い。 回転対称ともいう。 アルファベットでいうと 言葉よりも図で説明

線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
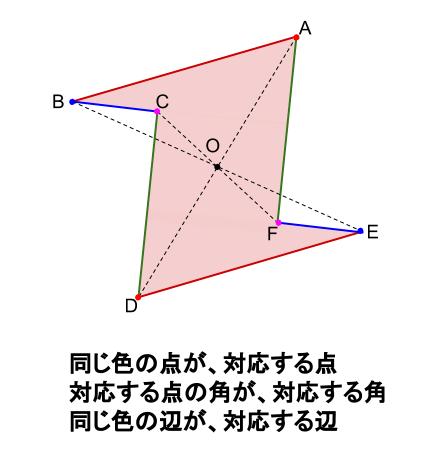
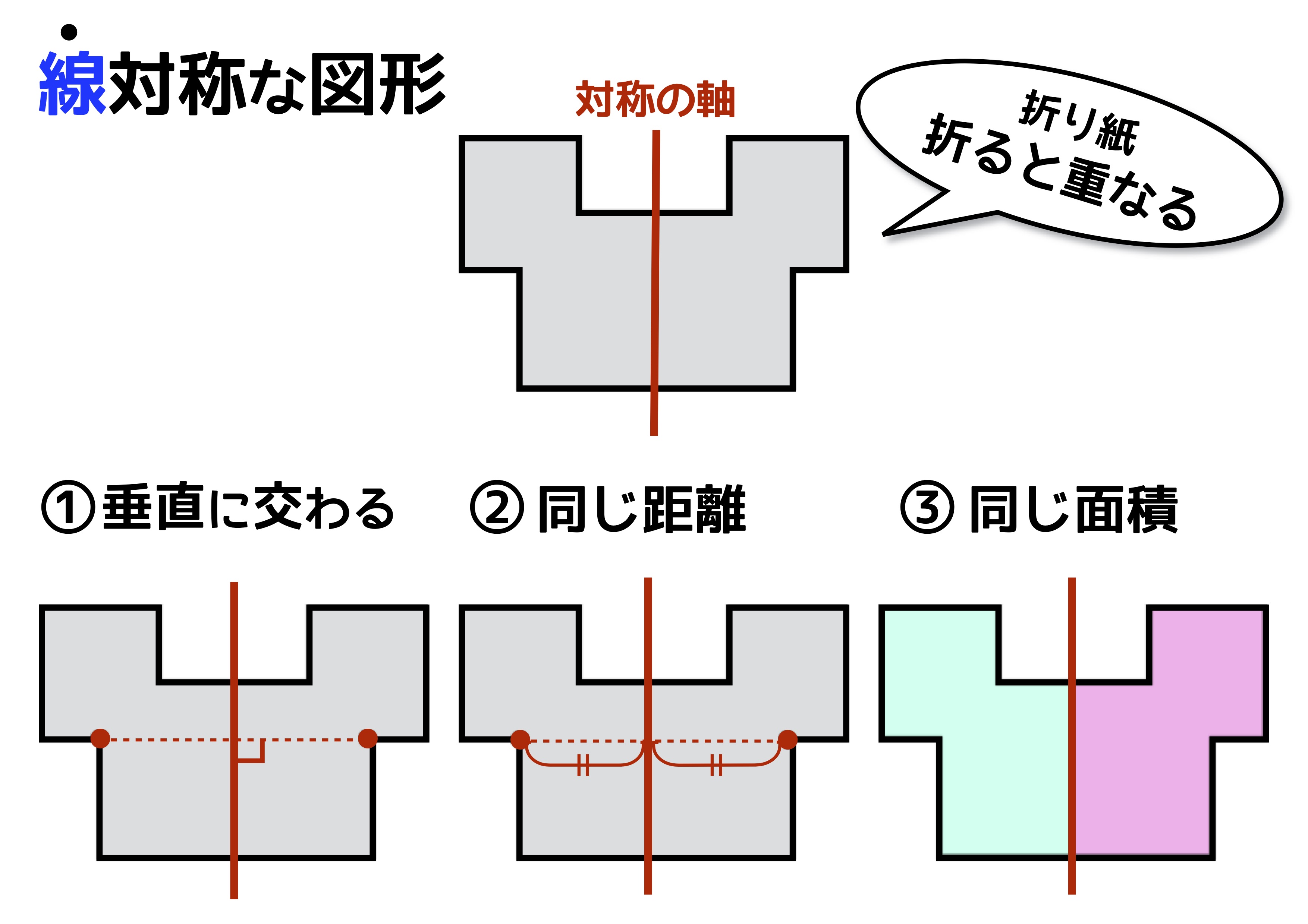
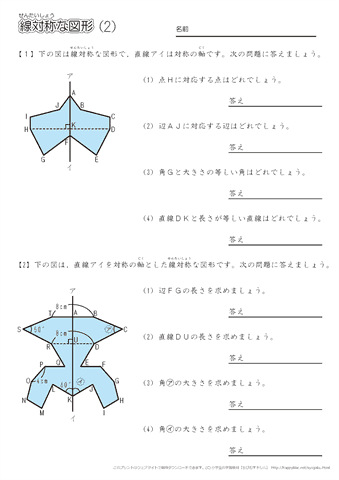
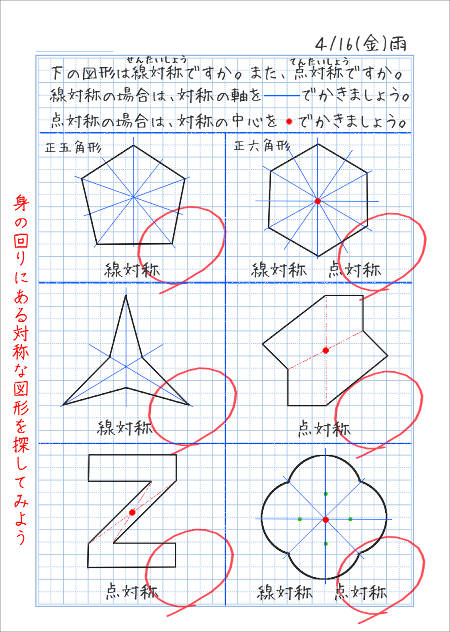
線対称な図形 点対称な図形 2 下の図は線対称な図形です。 ⑴ 対称の軸は,どれですか。 ⑵ 点Fに対応する点は,どれですか。 ⑶ 直線BCに対応する直線は,どれですか。 ⑷ 直線AJと直線KLはどのように交わっていますか。 3 下の図は点対称な図形です。 ⑴ 対称の中心は,どれですか。 ⑵ 点Dに精選版 日本国語大辞典 線対称の用語解説 〘名〙① 二つの平面図形の関係をいう語。二つの平面図形F、F′の点が一対一に対応し、対応する二点を結ぶ線分の垂直二等分線がつねに一定の直線lに一致するとき、FとF′とは直線lに関して線対称であるという。点対称な図形では、対応する点を結ぶ線分は対称の中心を通り、対称の中心によって 二等分 されます。また、線対称な図形の対称軸が複数存在する場合があるのに対して、 点対称な図形の対称の中心は \(\boldsymbol{1}\) つしか存在しません 。
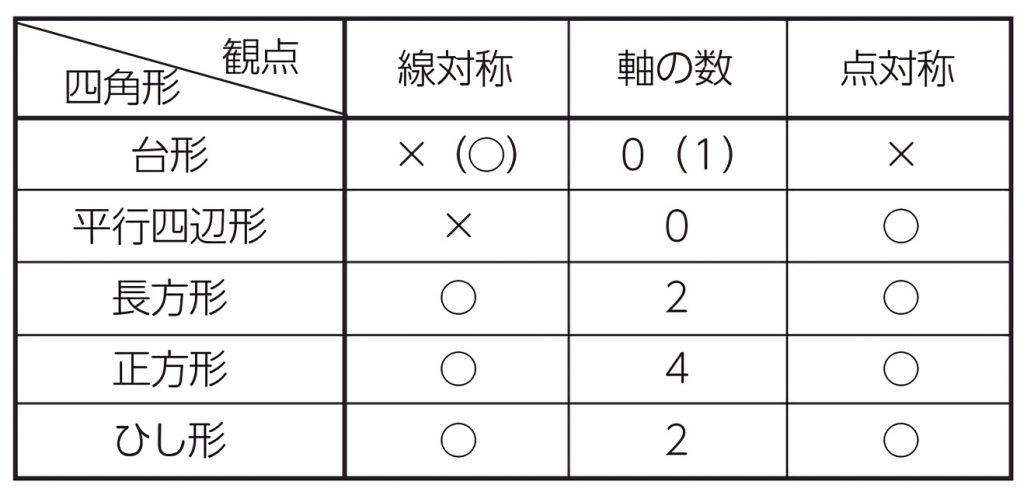
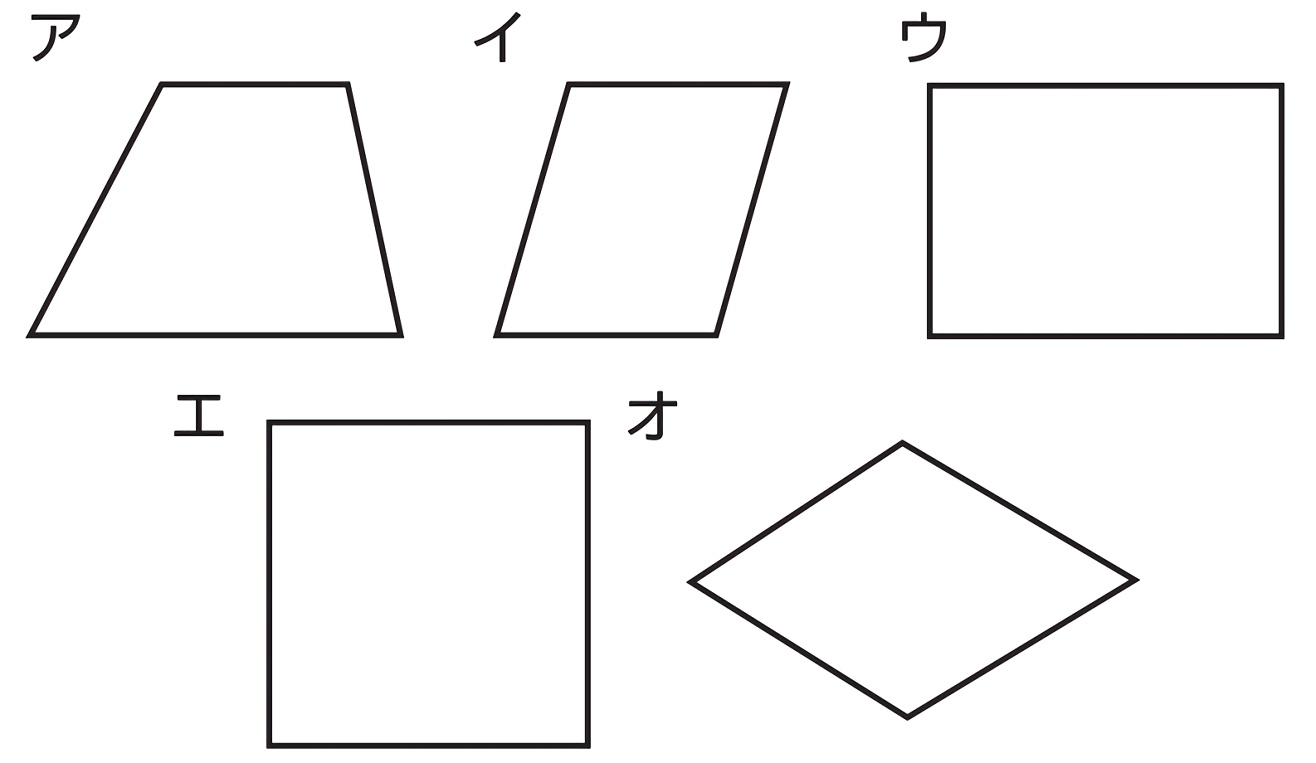
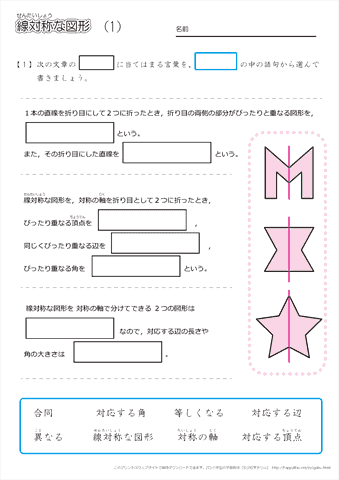
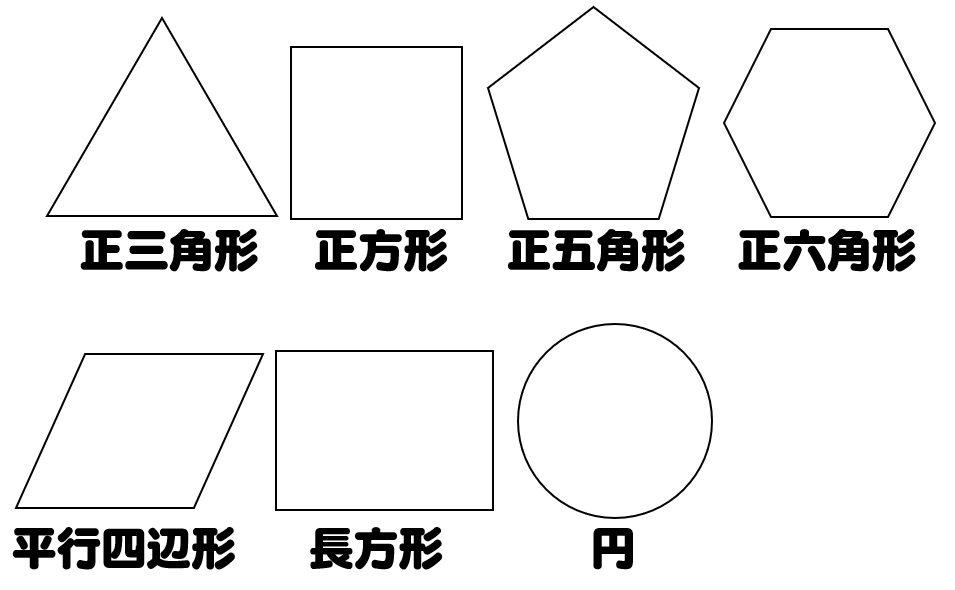
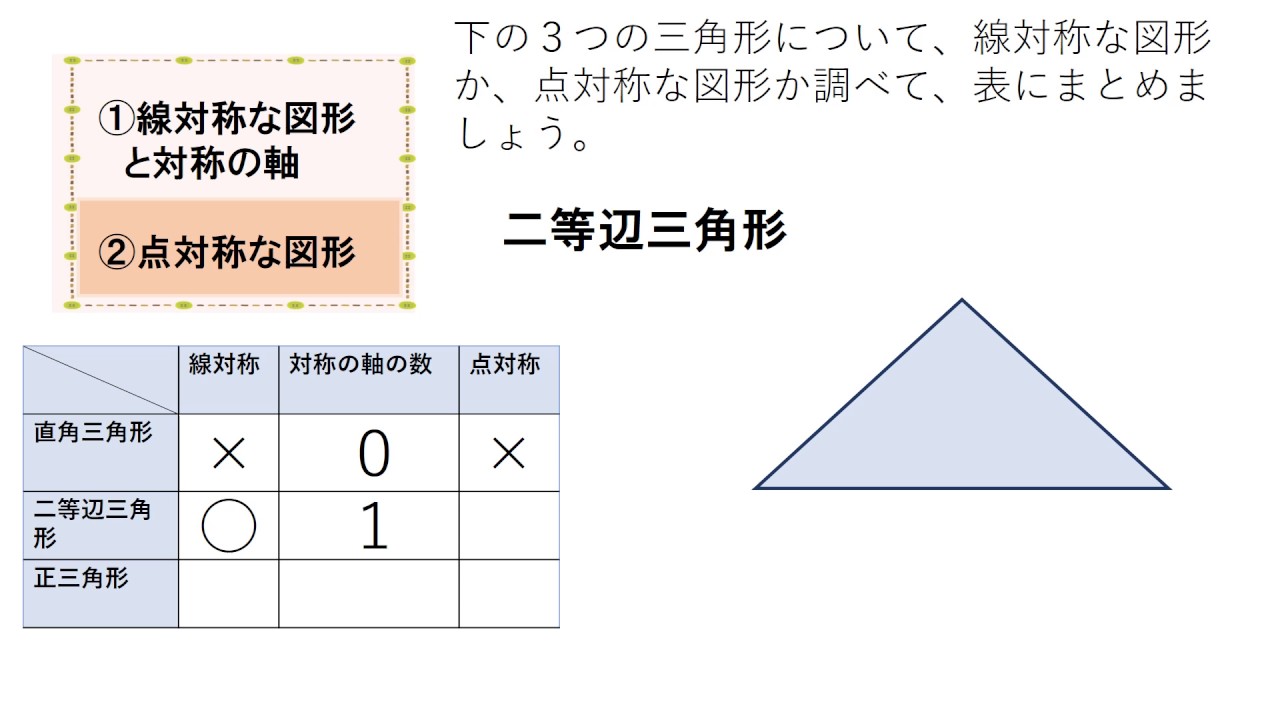
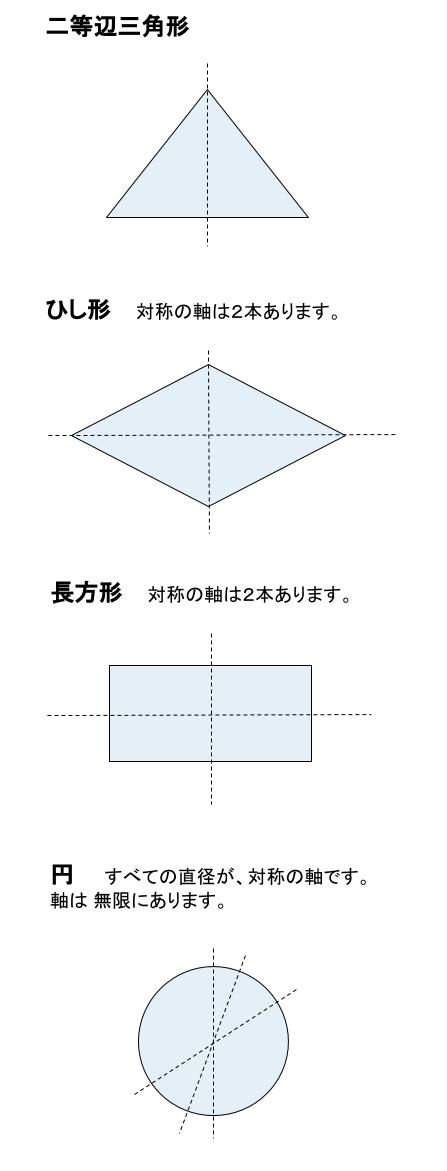
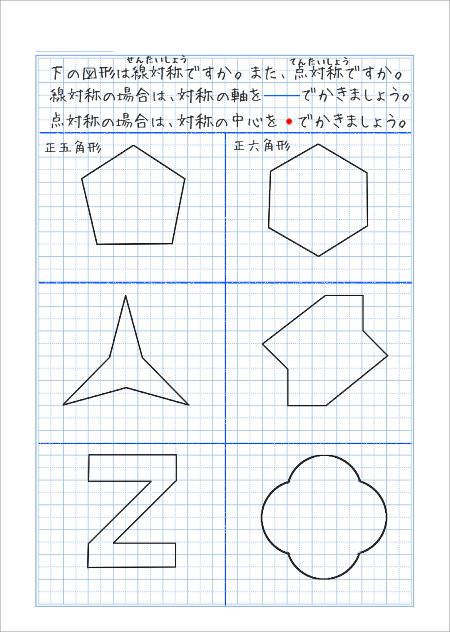
1 対称(多角形と対称) 1 これまでに学習した図形を,線対称・点対称で仲間分けして みましょう。 形の名前 線対称なら 対称の軸の本数 (図にかき入れよう) 点対称なら あ い う え お か き く ひとつだけ ぬりましょう。 やさしかった ふつう平面図形の対称 一つの平面図形を一定点の周りにα度回転してできる図形を、初めの図形にα度回転対称な図形といい、その定点を回転対称の中心という( 図b )。 180度回転対称な二つの図形はその中心に関して点対称であるという。一つの図形の一定直線に関する対称点をとってできる図形⑴ 線対称や点対称の図形の美しさに関心をもち,線対称や点対称の観点を用いて意欲的に操作活動 に取り組み,自分なりの「問い」を連続・発展させていこうとすることができる。 ⑵ ・ 線対称や点対称の図形の性質を考察する活動を通して,仲間分けをしていく集合の考えや対 応する点や辺
線対称 点対称 図形のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 | ||
「線対称 点対称 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「線対称 点対称 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「線対称 点対称 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「線対称 点対称 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「線対称 点対称 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「線対称 点対称 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「線対称 点対称 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「線対称 点対称 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「線対称 点対称 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「線対称 点対称 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「線対称 点対称 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 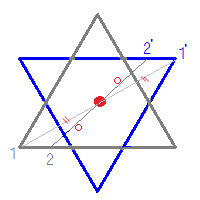 |
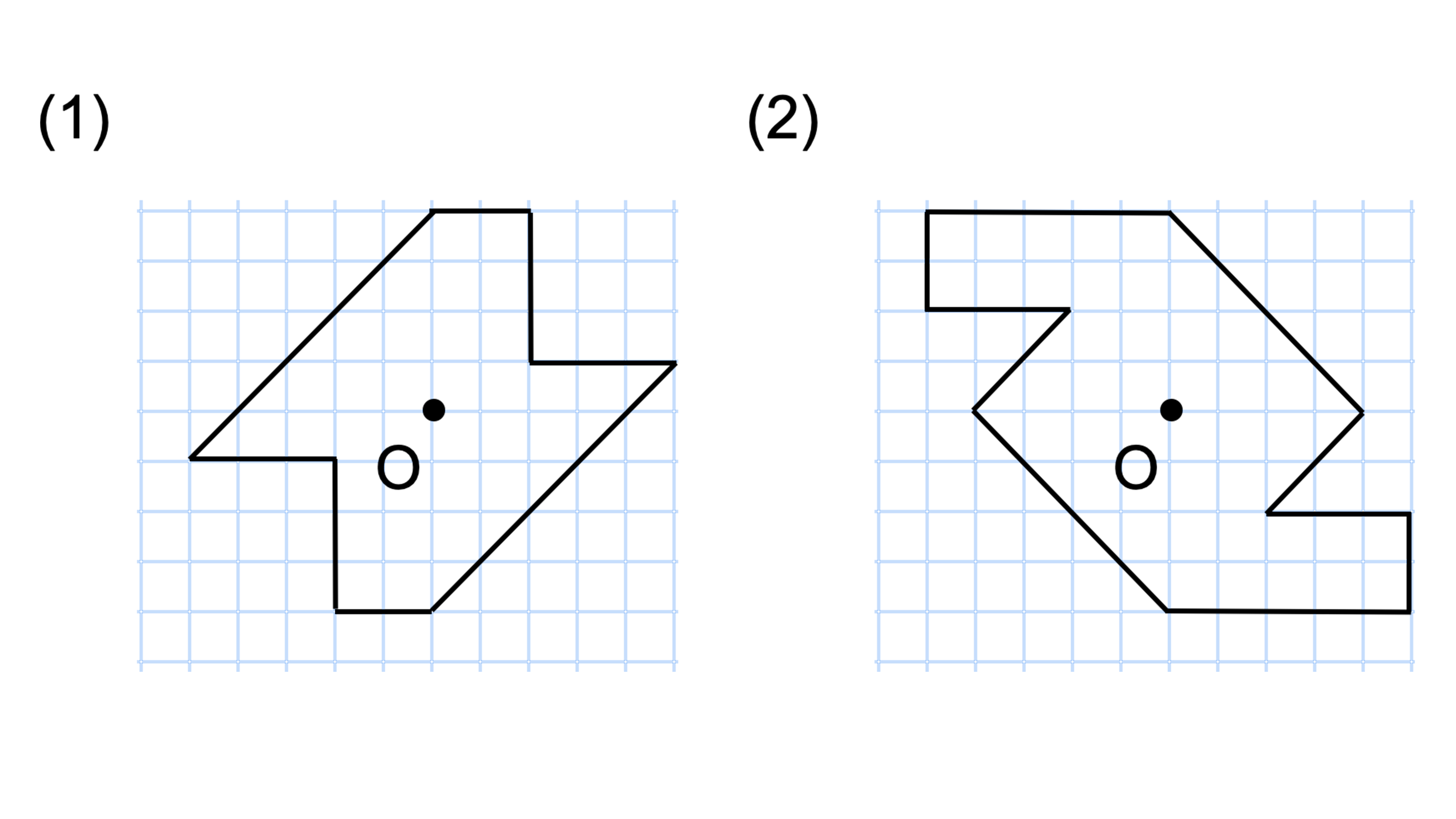
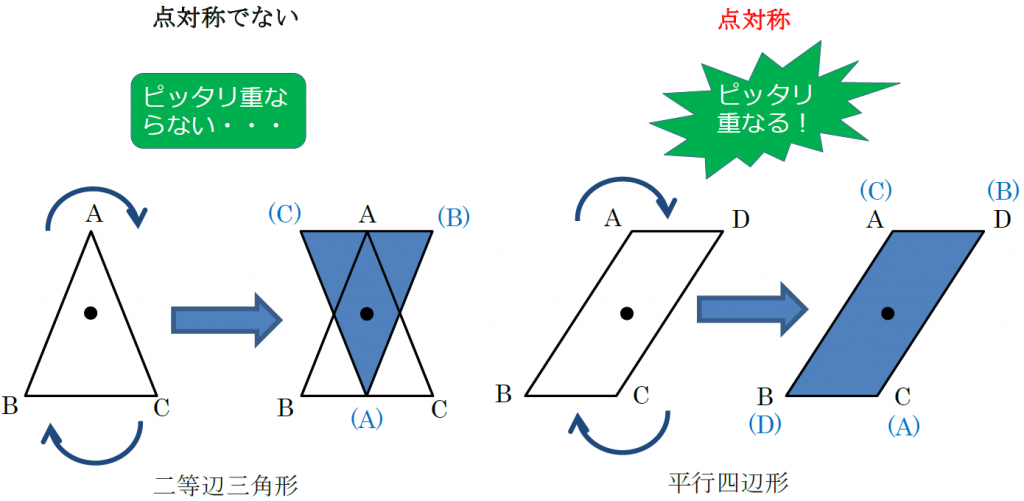
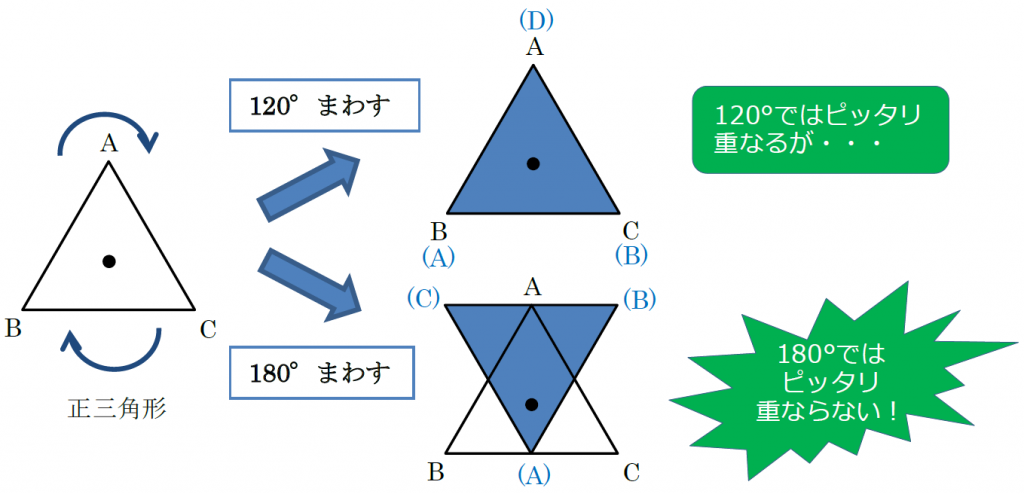
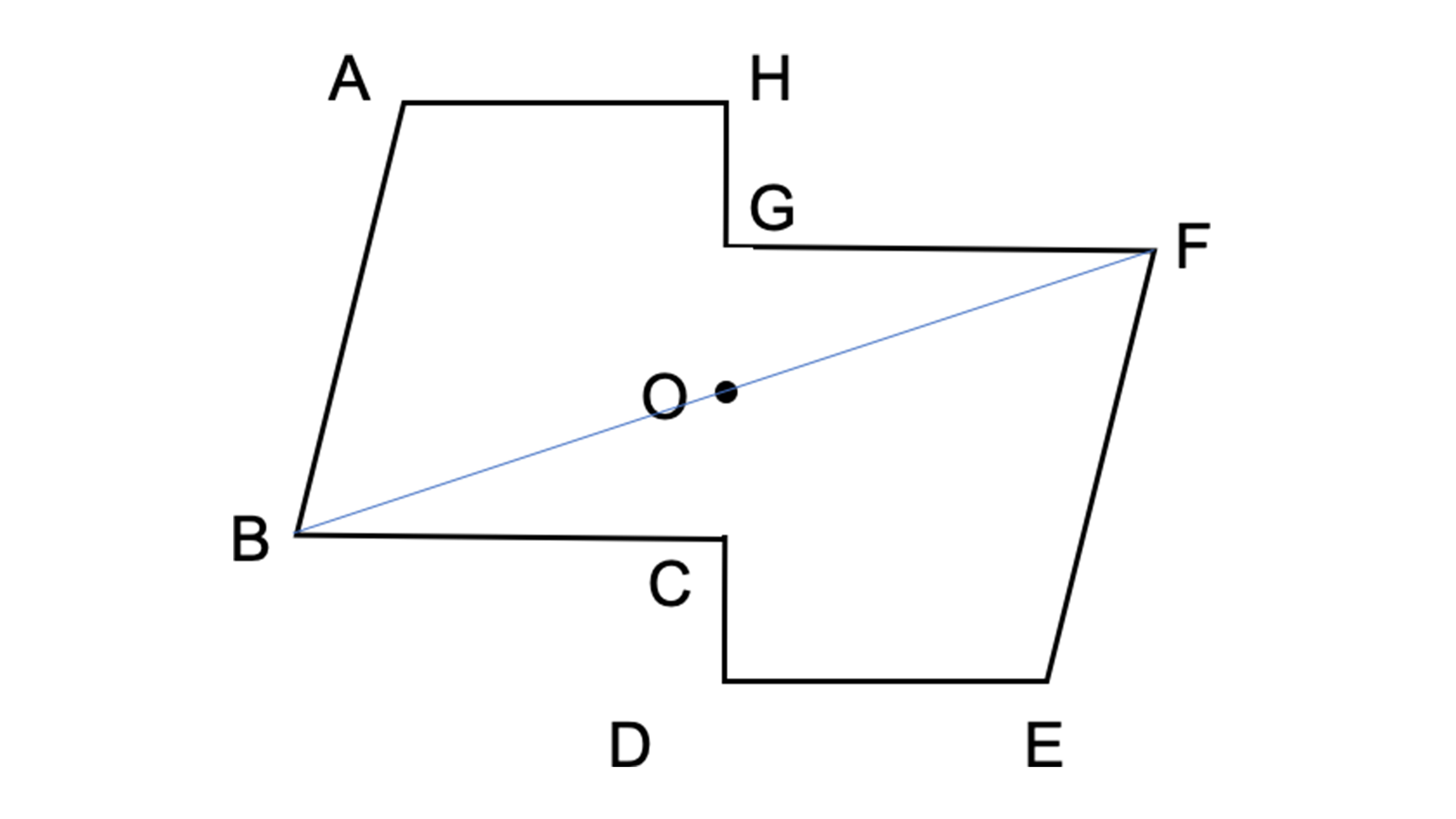
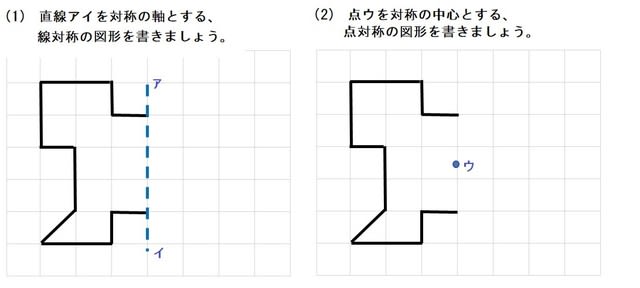
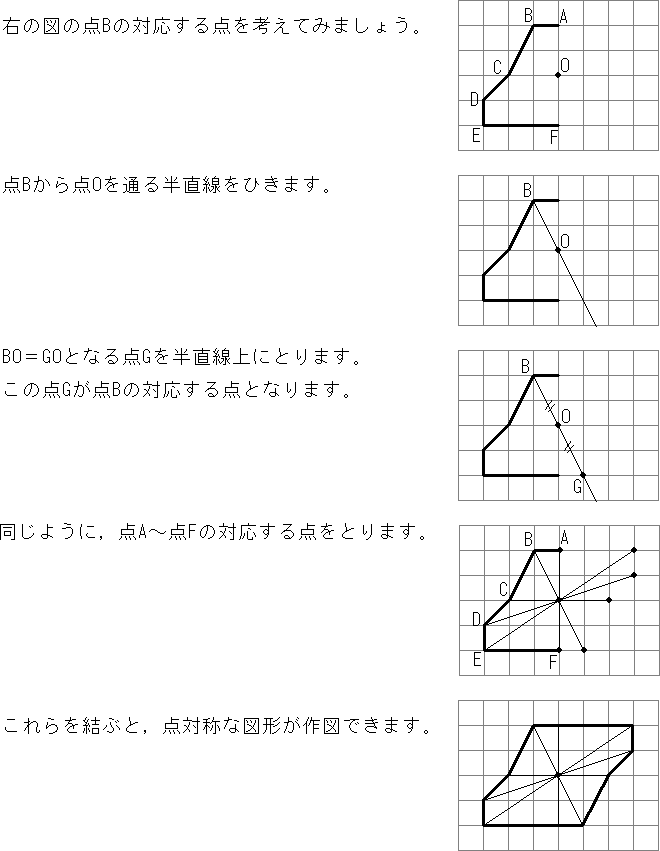
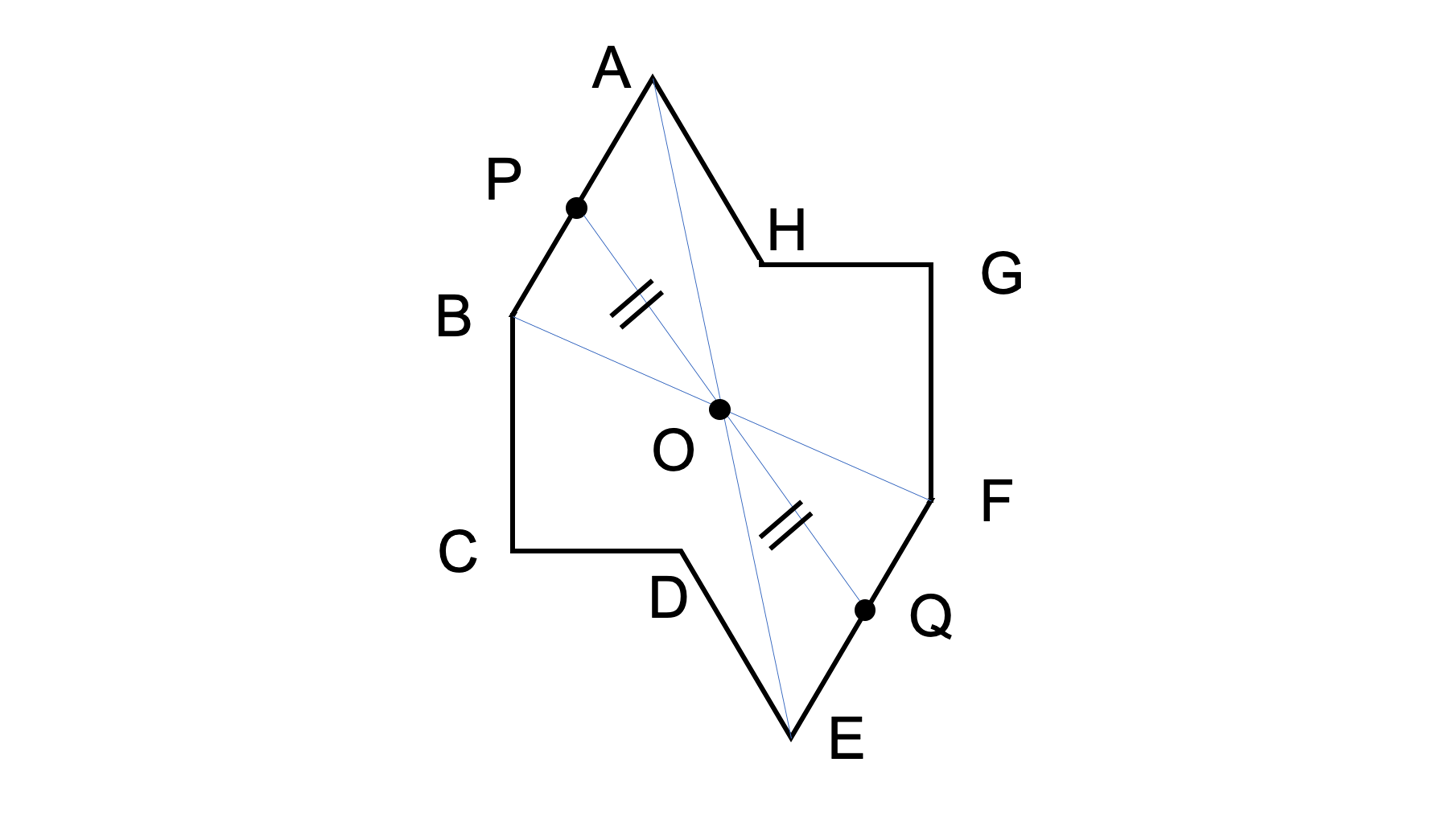
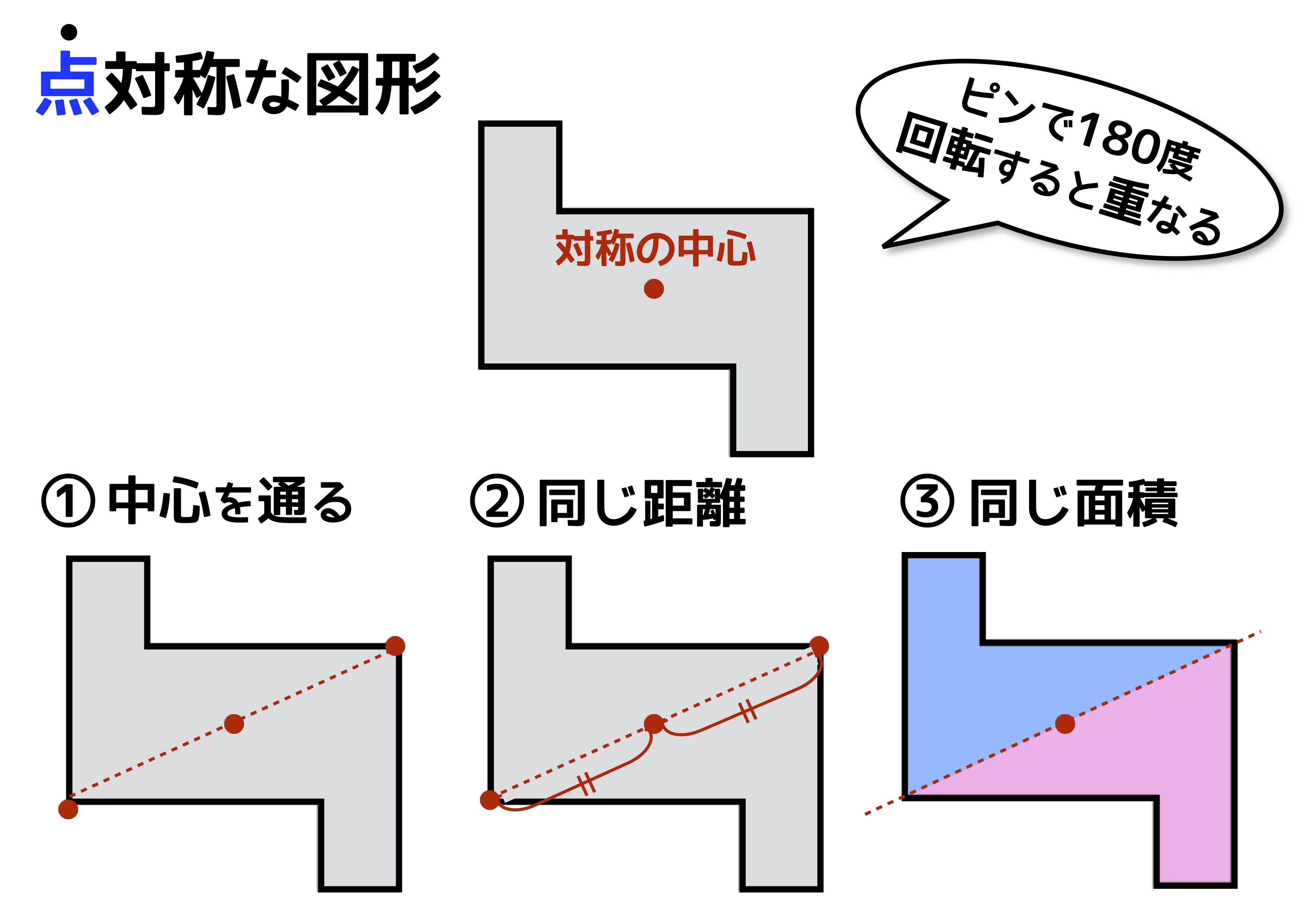
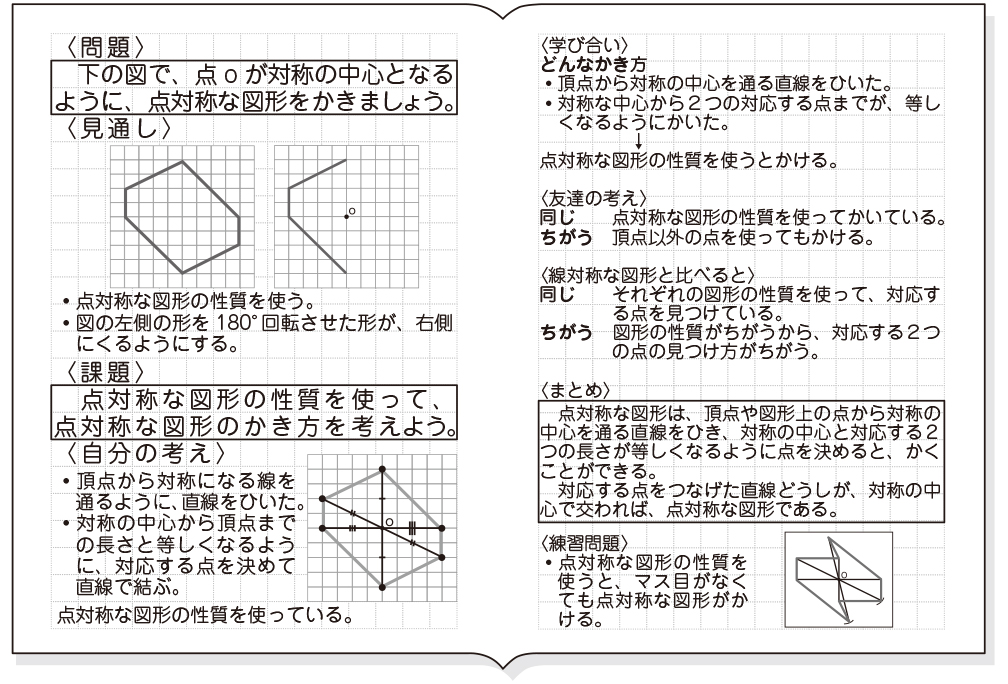
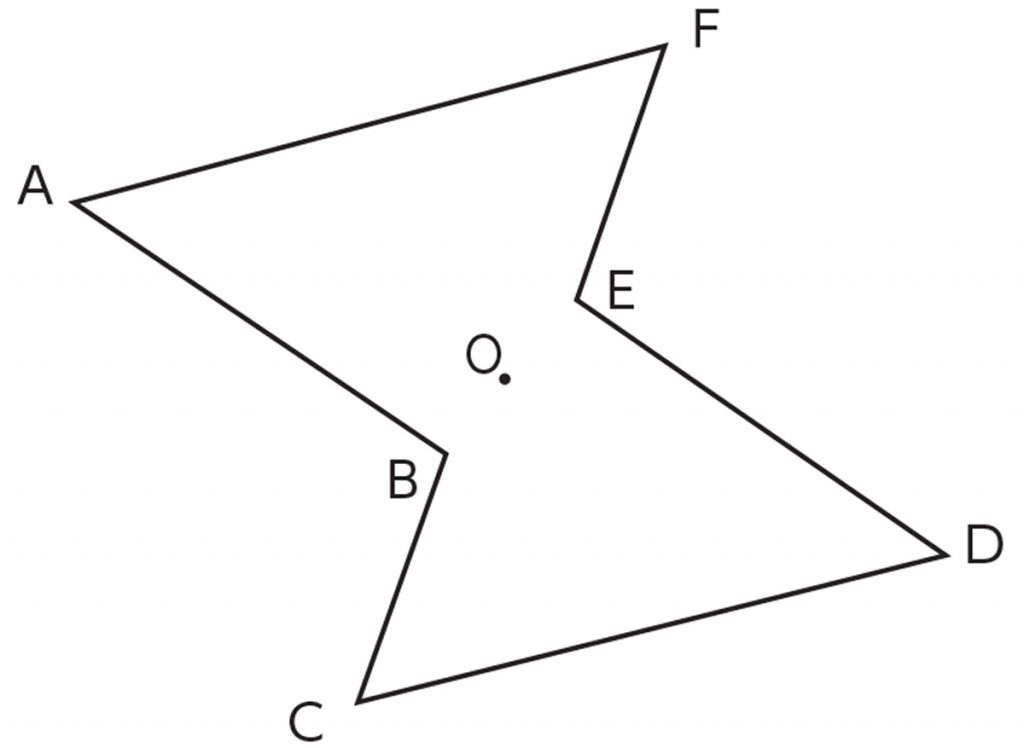
点対称な図形 解説 次の図のように,ある点を中心に180°回転させたとき,元の図形と一致する図形を 点対称な図形 といいます。 このとき回転の中心となる点を 対称の中心 といいます。 右の図は平行四辺形が対角線の交点を対称の中心とする点対称な 線対称な図形であることに変わりはないですが、対称の軸は次のような1本だけとなります。 円が1つのときは、円の中心を通る直線が対称の軸でした。円が2つのときは、円の中心を両方とも通る直線が対称の軸となります。 ここで、次のように、2つの円の中心を点 A, B とおき、2つの円の
コメント
コメントを投稿